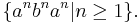Two-level grammar
A two-level grammar is a formal grammar that is used to generate another formal grammar [1], such as one with an infinite rule set [2]. This is how a Van Wijngaarden grammar was used to specify Algol68 [3]. A context free grammar that defines the rules for a second grammar can yield an effectively infinite set of rules for the derived grammar. This makes such two-level grammars more powerful than a single layer of context free grammar, because generative two-level grammars have actually been shown to be Turing complete.[1]
Two-level grammar can also refer to a formal grammar for a two-level formal language, which is a formal language specified at two levels, for example, the levels of words and sentences.
Contents |
Example
A well-known non-context-free language is
A two-level grammar for this language is the metagrammar
- N ::= 1 | N1
- X ::= a | b
together with grammar schema
- Start ::=
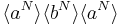
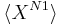 ::=
::= 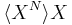
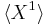 ::= X
::= X
See also
References
- ^ Sintzoff, M. "Existence of van Wijngaarden syntax for every recursively enumerable set", Annales de la Société Scientifique de Bruxelles 2 (1967), 115-118.
External links
- Petersson, Kent (1990), "Syntax and Semantics of Programming Languages", Draft Lecture Notes, PDF text.